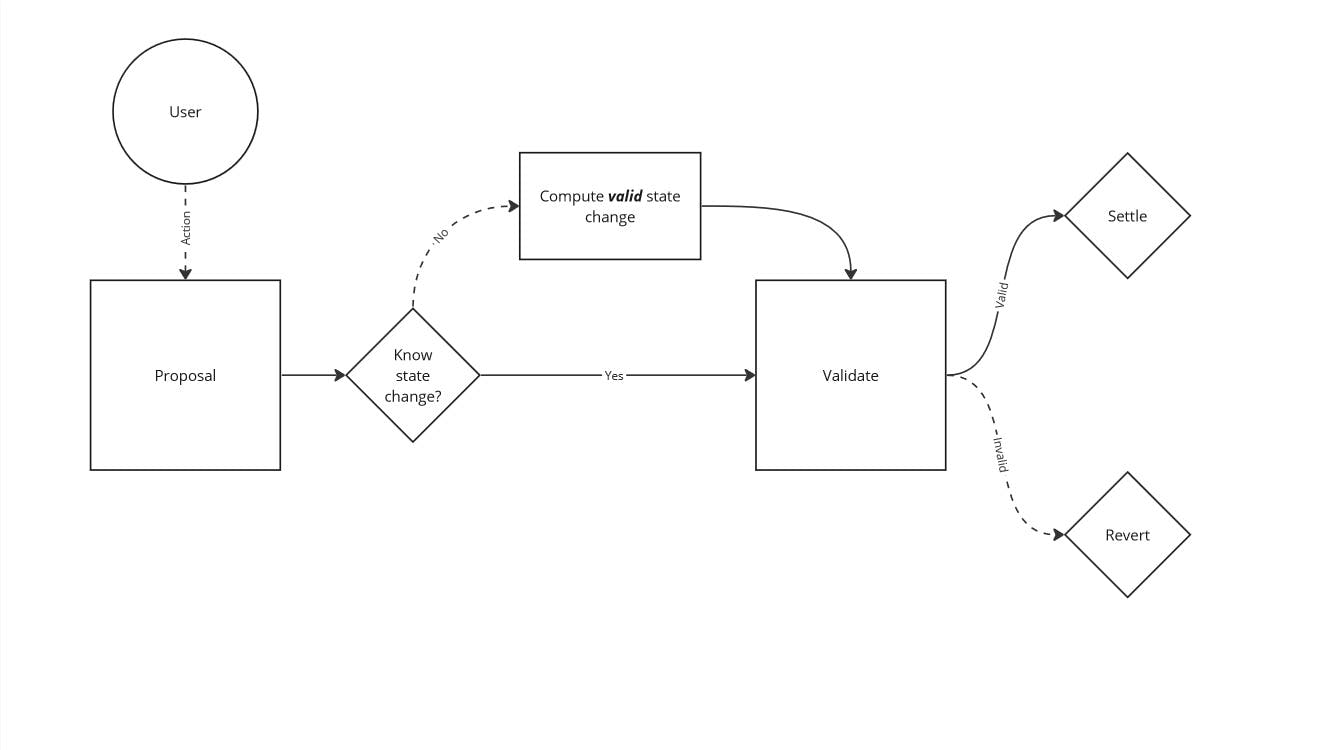
Technical Overview of DFMM

Over the past year, Primitive's developed a new set of smart contracts that are built on the strongest foundation available to smart contract developers: invariants. Invariants are rules inside a protocol that cannot be broken; if they are broken from a state change, the protocol should immediately revert the transaction. Invariants are integral to many existing protocols today, especially the automated market makers (AMMs), which is evidence that they are resilient against the adversaries that are present onchain.

This post will explain the core invariant securing the DFMM protocol and why this design can withstand the most common attack vectors being exploited in DeFi today.

The Invariant

Invariants can be general rules, even as simple as only allowing transactions during a certain time of day. For DFMM, the invariants are all mathematical based, which makes it so that there is a reference answer that is definitely true. A mathematical based invariant has a clear condition for being invalid, making it much more straightforward to find those invalid answers.

The DFMM protocol is capable of leveraging any invariant that is re-formulated into the mathematical structure we defined in the previous blog post. For this post, we are diving into the implementation, so here is one real example of a DFMM invariant in the code:

    function tradingFunction(
        uint256 rX,
        uint256 rY,
        uint256 L,
        G3M.G3MParams memory params
    ) internal pure returns (int256) {
        uint256 a = uint256(int256(rX.divWadDown(L)).powWad(int256(params.wX)));
        uint256 b = uint256(int256(rY.divWadDown(L)).powWad(int256(params.wY)));

        return int256(a.mulWadUp(b)) - int256(1 ether);
    }

There is a core DFMM smart contract at the heart of this system that will call these validate functions to verify operations. Any external smart contract can implement these functions with their own custom invariants and it would be supported by the core DFMM contract. For this example, let's break down this function into its components and explain why it's implemented this way.

Inputs

There are two "specialized" inputs that are for the DFMM architecture, a target address and pool_id. The address can be used by smart contracts that implement their own invariants to leverage some external contracts, if desired. A pool_id is needed to interact with a desired pool that exists in the DFMM smart contract.

There is a generalized input data that can contain anything. Having a generalized input like this makes it possible to integrate all kinds of invariants into the core DFMM system, as any information can be transmitted via that data input.

Note that the security of invariants are not handled by the DFMM contract. Instead, the DFMM contract delegates security responsibility to the external smart contract that implements the rule. DFMM only knows how to process the invariant validation logic. It's designed this way on purpose to make it easy to build and improve invariants.

Validation

    int256 constant EPSILON = 20;

    function validateAllocateOrDeallocate(
        address,
        uint256 poolId,
        bytes calldata data
    ) ... {
        (reserveX, reserveY, totalLiquidity) =
            abi.decode(data, (uint256, uint256, uint256));

        invariant = tradingFunction(
            reserveX,
            reserveY,
            totalLiquidity,
            abi.decode(getPoolParams(poolId), (G3MParams))
        );

        valid = -(EPSILON) < invariant && invariant < EPSILON;
    }

The next part of the code is where the external contract validates the invariant. In this code, it's using the tradingFunction method, which computes a value based on the token reserves, liquidity, and parameters of a G3M pool. If you want to get a better understanding of this specific mathematical formula, we recommend reading the previous post on Dynamic Function Market Makers.

After computing a value, we check if this output is within a valid range. We've determined a valid range for this formula to be between -20 wei and +20 wei, which is still being tested upon. This returns a boolean that is used by the DFMM core contract to determine if the transaction should continue to be executed or reverted.

DFMM Finalization

Here is where DFMM will utilize the result of this validation:

    function allocate(
        uint256 poolId,
        bytes calldata data
    ) ... {
        (uint256 deltaX, uint256 deltaY, uint256 deltaL) =
            _updatePoolReserves(poolId, true, data);

        ...
    }


    function _updatePoolReserves(
        uint256 poolId,
        bool isAllocate,
        bytes calldata data
    ) ... {
        (
            bool valid,
            int256 invariant,
            uint256 adjustedReserveX,
            uint256 adjustedReserveY,
            uint256 adjustedTotalLiquidity
        ) = IStrategy(pools[poolId].strategy).validateAllocateOrDeallocate(
            msg.sender, poolId, data
        );

        if (!valid) {
            revert Invalid(invariant < 0, abs(invariant));
        }

        ...
    }

A nice attribute of this code is that it matches identically to the explanation of the invariant in the opening paragraph of this post. It's really as simple as doing the validation check and reverting the transaction if it fails. That is what happens in the first line of code executed in this allocate operation.

For context, the allocate operation is one of three operations that can be executed via the DFMM contract to provide liquidity to a pool. The other two operations are deallocate (remove liquidity) and swap.

This validation method also returns the new state of each reserves and the pool's liquidity. If the condition is valid, the new reserve state is used to compute the quantity of tokens to send to or request from the user.

    function _updatePoolReserves(
        uint256 poolId,
        bool isAllocate,
        bytes calldata data
    ) ... {
        ...

        deltaX = isAllocate
            ? adjustedReserveX - pools[poolId].reserveX
            : pools[poolId].reserveX - adjustedReserveX;
        deltaY = isAllocate
            ? adjustedReserveY - pools[poolId].reserveY
            : pools[poolId].reserveY - adjustedReserveY;
        deltaL = isAllocate
            ? adjustedTotalLiquidity - pools[poolId].totalLiquidity
            : pools[poolId].totalLiquidity - adjustedTotalLiquidity;

        _manageTokens(poolId, isAllocate, deltaL);

        pools[poolId].reserveX = adjustedReserveX;
        pools[poolId].reserveY = adjustedReserveY;
        pools[poolId].totalLiquidity = adjustedTotalLiquidity;
    }

Finally, the state changes get settled via the _manageTokens method and in the last lines of _updatePoolReserves method. For posterity, _manageTokens is a dedicated function for making state changes to the liquidity and its respective liquidity token:

    function _manageTokens(
        uint256 poolId,
        bool isAllocate,
        uint256 deltaL
    ) internal {
        LPToken liquidityToken = LPToken(pools[poolId].liquidityToken);
        uint256 totalSupply = liquidityToken.totalSupply();
        uint256 totalLiquidity = pools[poolId].totalLiquidity;

        if (isAllocate) {
            uint256 amount =
                deltaL.mulWadDown(totalSupply.divWadDown(totalLiquidity));
            liquidityToken.mint(msg.sender, amount);
        } else {
            uint256 amount =
                deltaL.mulWadUp(totalSupply.divWadUp(totalLiquidity));
            liquidityToken.burn(msg.sender, amount);
        }
    }

Once the state changing code is reached, all conditions have already been validated. This is the "effects" part of the standard practice in smart contract design, called the "checks, effects, interactions" pattern.

Note that the allocate and deallocate operations carry the lock modifier on their functions, preventing the operations from being executed again within the same frame of execution.

    /// @dev Prevents reentrancy.
    modifier lock() {
        if (_locked == 2) revert Locked();
        _locked = 2;
        _;
        _locked = 1;
    }

The Swap Operation

The DFMM deallocate operation is the opposite of allocate, removing assets from a DFMM liquidity pool. Both these operations are simple, because they either increase (allocate) or decrease (deallocate) both reserves, do not have to compute or handle fees, and have basic settlement mechanics for the liquidity. The swap operation in DFMM is the most complicated because the reserves, fees, and liquidity all change while interacting with eachother. Overall, the structure of the code is remains similar for the G3M invariant:

    function validateSwap(
        address,
        uint256 poolId,
        bytes memory data
    )
        external
        view
        returns (
            bool valid,
            int256 invariant,
            int256 liquidityDelta,
            uint256 nextRx,
            uint256 nextRy,
            uint256 nextL
        )
    {
        G3MParams memory params = abi.decode(getPoolParams(poolId), (G3MParams));

        (uint256 startRx, uint256 startRy, uint256 startL) =
            IDFMM(dfmm).getReservesAndLiquidity(poolId);

        (nextRx, nextRy, nextL) = abi.decode(data, (uint256, uint256, uint256));

        uint256 amountIn;
        uint256 fees;
        uint256 minLiquidityDelta;

        if (nextRx > startRx) {
            amountIn = nextRx - startRx;
            fees = amountIn.mulWadUp(params.swapFee);
            minLiquidityDelta += fees.mulWadUp(startL).divWadUp(startRx);
        } else if (nextRy > startRy) {
            amountIn = nextRy - startRy;
            fees = amountIn.mulWadUp(params.swapFee);
            minLiquidityDelta += fees.mulWadUp(startL).divWadUp(startRy);
        } else {
            revert("invalid swap: inputs x and y have the same sign!");
        }

        uint256 poolId = poolId;

        liquidityDelta = int256(nextL)
            - int256(
                G3MLib.computeNextLiquidity(
                    startRx, startRy, abi.decode(getPoolParams(poolId), (G3MParams))
                )
            );

        invariant = G3MLib.tradingFunction(nextRx, nextRy, nextL, params);
        valid = -(EPSILON) < invariant && invariant < EPSILON;
    }

In the swap operation, one reserve is increasing while the other decreases. The validation then checks if they changed enough in either direction to be considered valid. This is the most critical step in the execution of the operation as it determines the price of the tokens during the swap. The first if statement determines the direction by looking at which reserve increased.

Once that is determined, the fees are computed by multiplying the quantity of tokens being traded by the percentage swap fee: fees = amountIn.mulWadUp(params.swapFee). This is a standard mechanism employed by Automated Market Makers (AMM) to charge swap fees by reducing the purchasing power of a desired trade. In this specific invariant of G3M, the liquidity is also expected to grow by the proportion of the fees relative to the underlying reserve. The liquidity of a pool is correlated to the fees, i.e. as fees grow the liquidity grows.

During the swap operation, it's possible for the underlying liquidity to change because it's a dynamic function market maker. When swap operations are requested, there has to be a valid new liquidity value that considers and computes how much the liquidity is expected to change. Liquidity is used as a mechanism to make pricing changes to the pool (dynamic) based on other conditions, like timestamps. While the liquidityDelta value is not used in the validation (because the nextL is used), it's a useful value to determine how accurate the pre-computed liquidity value was.

Going back to the core DFMM contract, there is a dedicated _settle function that is responsible for altering the reserves and transferring the tokens:

    function swap(
        uint256 poolId,
        bytes calldata data
    ) ... {
        (
            bool valid,
            int256 invariant,
            ,
            uint256 adjustedReserveX,
            uint256 adjustedReserveY,
            uint256 adjustedTotalLiquidity
        ) = IStrategy(pools[poolId].strategy).validateSwap(
            msg.sender, poolId, data
        );

        if (!valid) {
            revert Invalid(invariant < 0, abs(invariant));
        }

        pools[poolId].totalLiquidity = adjustedTotalLiquidity;

        (bool isSwapXForY,,, uint256 inputAmount, uint256 outputAmount) =
            _settle(poolId, adjustedReserveX, adjustedReserveY);

        ...
    }

    function _settle(
        uint256 poolId,
        uint256 adjustedReserveX,
        uint256 adjustedReserveY
    )
        ...
    {
        uint256 originalReserveX = pools[poolId].reserveX;
        uint256 originalReserveY = pools[poolId].reserveY;

        isSwapXForY = adjustedReserveX > originalReserveX;

        if (isSwapXForY) {
            if (adjustedReserveY >= originalReserveY) revert InvalidSwap();
            inputToken = pools[poolId].tokenX;
            outputToken = pools[poolId].tokenY;
            inputAmount = adjustedReserveX - originalReserveX;
            outputAmount = originalReserveY - adjustedReserveY;
        } else {
            if (adjustedReserveX >= originalReserveX) revert InvalidSwap();
            inputToken = pools[poolId].tokenY;
            outputToken = pools[poolId].tokenX;
            inputAmount = adjustedReserveY - originalReserveY;
            outputAmount = originalReserveX - adjustedReserveX;
        }

        // Do the state updates to the reserves before calling untrusted addresses.
        pools[poolId].reserveX = adjustedReserveX;
        pools[poolId].reserveY = adjustedReserveY;

        uint256 preInputBalance = ERC20(inputToken).balanceOf(address(this));
        uint256 preOutputBalance = ERC20(outputToken).balanceOf(address(this));

        _transferFrom(inputToken, inputAmount);
        _transfer(outputToken, msg.sender, outputAmount);

        uint256 postInputBalance = ERC20(inputToken).balanceOf(address(this));
        uint256 postOutputBalance = ERC20(outputToken).balanceOf(address(this));

        if (postInputBalance < preInputBalance + inputAmount) {
            revert InvalidSwapInputTransfer();
        }

        if (postOutputBalance < preOutputBalance - outputAmount) {
            revert InvalidSwapOutputTransfer();
        }

        return (isSwapXForY, inputToken, outputToken, inputAmount, outputAmount);
    }

The _settle function is not doing anything extra special, it just requires extra logic to determine which reserve to change and whether or not to transfer tokens out or request them from the user. All this code highlights the benefits of building a protocol from a foundation of invariants: logic is kept simple to do the job while the invariants do the heavy lifting. Almost all of the logic outside of the invariant validation is just enough code to get the job done.

Validating the Invariant

We've had a real experience of finding scenarios where invariant conditions we've designed could be tricked into producing a valid result with invalid inputs. The consequences of this are severe, because it can easily lead to full exploitation of the assets secured by the invariant. Making sure an invariant is strong is the difficult part, as it requires a massive amount of testing across as many scenarios as possible. A future blog post will go into more detail in the process of invariant validation and testing.

Invariant Computation

The real example we walked through in the previous paragraphs had a lot of simple computation because of the underlying invariant's simplicity. The invariant utilized basic arithmetic, making it straightforward to compute new state changes before validating them in real transactions. However, not all mathematically based invariants could be clean enough to only contain arithmetic. For Primitive, we've been building a mathematical invariant that uses transcendental functions, which basically don't have exact outputs, only approximations. These approximations scale off eachother, quickly causing error to exponentially grow leading to weak invariants.

Here is the formula used by the LogNormal strategy that will be compatible with the DFMM protocol on release:

    function tradingFunction(
        uint256 rx,
        uint256 ry,
        uint256 L,
        LogNormal.LogNormalParams memory params
    ) internal pure returns (int256) {
        require(rx < L, "tradingFunction: invalid x");

        int256 AAAAA;
        int256 BBBBB;
        if (FixedPointMathLib.divWadDown(rx, L) >= ONE) {
            AAAAA = int256(2 ** 255 - 1);
        } else {
            AAAAA = Gaussian.ppf(int256(FixedPointMathLib.divWadDown(rx, L)));
        }
        if (
            FixedPointMathLib.divWadDown(
                ry, FixedPointMathLib.mulWadDown(params.strike, L)
            ) >= ONE
        ) {
            BBBBB = int256(2 ** 255 - 1);
        } else {
            BBBBB = Gaussian.ppf(
                int256(
                    FixedPointMathLib.divWadDown(
                        ry, FixedPointMathLib.mulWadDown(params.strike, L)
                    )
                )
            );
        }

        int256 CCCCC = int256(computeSigmaSqrtTau(params.sigma, params.tau));

        return AAAAA + BBBBB + CCCCC;
    }

What a formula. Without sharing all the code in the math library dependency, the takeaway is that these functions output results that are approximations of their true theoretical result. The problem with this is that a calculator on the internet will most likely return a different result, even with the same inputs. This makes it extremely difficult to make sure an invariant cannot be broken or tricked. The details of how this invariant is validated itself will be saved for a future blog post, for now we will go into how an onchain "solver" can compute state changes for these complicated formulas.

Computing State Changes

A state change for an invariant in this case means how the reserves and liquidity change. This affects everything on a liquidity pool, but most importantly the price of the tokes in the pool. For operations on DFMM, all state changes have to be pre-computed and basically requested to be made, after which DFMM will leverage the external strategy to validate the request. This model of requesting and validating state changes keeps the smart contracts in a fundamentally simple architecture.

With that said, the proposed state changes must be accurate, or else it will lead to transactions reverting. This carries a cost to users because they will pay for all the computation up to that point, and complicated invariants could require more computation. The best way to accurately compute a state change that will pass the invariant check is to do it in the same environment, in a smart contract.

In the DFMM codebase, the "solver" smart contracts are responsible for doing this. Here is the code for finding the correct reserves to propose when allocating a desired amount of X tokens, handled by the LogNormalSolver contract:

    function allocateGivenX(
        uint256 poolId,
        uint256 amountX
    ) public view returns (uint256, uint256, uint256) {
        (uint256 rx,, uint256 L) = getReservesAndLiquidity(poolId);
        (uint256 nextRx, uint256 nextL) =
            computeAllocationGivenX(true, amountX, rx, L);
        
        ...
    }

    function getNextLiquidity(
        uint256 poolId,
        uint256 rx,
        uint256 ry,
        uint256 L
    ) public view returns (uint256) {
        bytes memory data = abi.encode(rx, ry, L);
        int256 invariant = IStrategy(strategy).computeSwapConstant(poolId, data);
        return
            computeNextLiquidity(rx, ry, invariant, L, fetchPoolParams(poolId));
    }

This code will eventually reach the point where it needs to search the potential space for valid reserves, at the computeNextLiquidity method:

function computeNextLiquidity(
    uint256 rx,
    uint256 ry,
    int256 invariant,
    uint256 approximatedL,
    LogNormal.LogNormalParams memory params
) pure returns (uint256 L) {
    uint256 upper = approximatedL;
    uint256 lower = approximatedL;
    int256 computedInvariant = invariant;
    if (computedInvariant < 0) {
        while (computedInvariant < 0) {
            lower = lower.mulDivDown(999, 1000);
            computedInvariant = LogNormalLib.tradingFunction({
                rx: rx,
                ry: ry,
                L: lower,
                params: params
            });
        }
    } else {
        while (computedInvariant > 0) {
            upper = upper.mulDivUp(1001, 1000);
            computedInvariant = LogNormalLib.tradingFunction({
                rx: rx,
                ry: ry,
                L: upper,
                params: params
            });
        }
    }
    L = bisection(
        abi.encode(rx, ry, computedInvariant, params),
        lower,
        upper,
        uint256(EPSILON),
        MAX_ITER,
        findRootLiquidity
    );
}

Let's walk through what this code is doing and how it produces very accurate results that we can use to propose allocate operations.

The first step in the code is an if statement that establishes the boundaries to search between. The LogNormal invariant is designed to return 0, exactly. It's possible for it to be slightly positive or negative, but the 0 is the theoretically ideal result.

In both cases, the liquidity value is being changed until the result flips it sign. Once that point is reached, we've reached an endpoint of our search space. In the last line of code, a bisection function is being called using a few parameters.

• The actual data is encoded into a generalized packet of bytes.
• The lower and upper bounds of inputs to search between.
• A "distance" between the result of an input and the target result of 0 that is accepted as valid.
• A maximum number of iterations to run during the bisection.
• The function that is being searched for a root, i.e. an input that will produce a 0 output.

Ideally, a liquidity value is found that when combined with the respective proposed reserves rx and ry, invariant, and strategy parameters, produces a 0 invariant value. This will produce a valid result when the DFMM contract is executing the operation.

These solvers are designed to be used in an off-chain setting to find the exact numbers to provide the DFMM smart contract system for the highest chance of successful transactions. Additionally, the solvers provide insight into one of the key security attributes of this invariant based architecture: being able to search for valid results in a streamlined way.

Invariant Systems are the Strongest Defense

This post has encapsulated the majority of the code that is used to implement the DFMM protocol and its features. One of the key takeaways from this overview is how powerful an invariant based system can be in securing smart contracts. Reducing the key operations that are available to execute inside a protocol down to a mathematical invariant has made it possible to search for invalid scenarios. This has proven to be an invaluable methodology to securing a protocol, both at a low-level security perspective and an economic perspective.